Trong bài này tôi sẽ thử nghiệm dịch vụ AI dưới dạng API của Anthropic (đơn vị chủ sở hữu của Claude AI) – là đối thủ chính của OpenAI hiện nay. Nhiệm vụ của quá trình thử nghiệm này là:
- Tích hợp API cho hệ thống Multi-Agent sử dụng AutoGen của Microsoft nhằm xây dựng một số agent thông minh (bằng cách sử dụng AI API) để tương tác với nhau giải quyết nhiệm vụ của giáo viên (teacher) và học sinh (student) để trao đổi về một chủ đề nào đó do người dùng (user) đặt ra.
- Chương trình được cấu hình với 02 hệ thống API của OpenAI và Anthropic để so sánh chi phí trong cùng một ngữ cảnh, câu hỏi.
- Model được sử dụng là : claude-3-5-sonnet-20241022 và gpt-4o-mini
Pricing
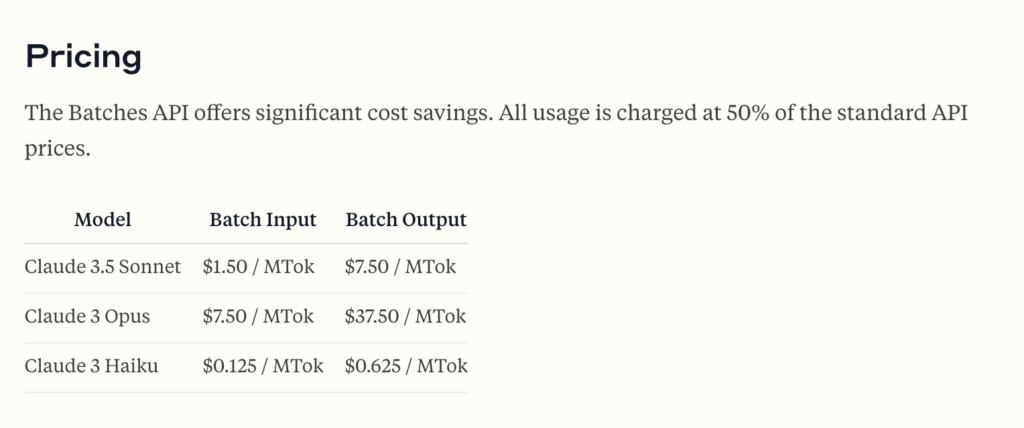
ANTHROPIC API
import os
from dotenv import load_dotenv
from autogen import ConversableAgent
import anthropic
# Load cấu hình từ file .env
load_dotenv()
# Sử dụng biến môi trường để lấy API key của Anthropic
api_key = os.getenv("ANTHROPIC_API_KEY")
model = 'claude-3-5-sonnet-20241022'
# Tạo các agent với cấu hình riêng cho Anthropic
student_agent = ConversableAgent(
name="Student_Agent",
system_message="You are a student willing to learn.",
llm_config={
"config_list": [
{
"model": model,
"api_type": "anthropic",
"base_url": "https://api.anthropic.com/v1",
"api_key": api_key
}
],
"max_tokens": 1000,
},
)
teacher_agent = ConversableAgent(
name="Teacher_Agent",
system_message="You are a math teacher explaining concepts clearly.",
llm_config={
"config_list": [
{
"model": model,
"api_type": "anthropic",
"base_url": "https://api.anthropic.com/v1",
"api_key": api_key
}
],
"max_tokens": 1000,
},
)
# Thực hiện chat giữa hai agent
chat_result = student_agent.initiate_chat(
teacher_agent,
message="Số phức là gì?",
summary_method="reflection_with_llm",
max_turns=2,
)
# In kết quả của cuộc trò chuyện
print(chat_result)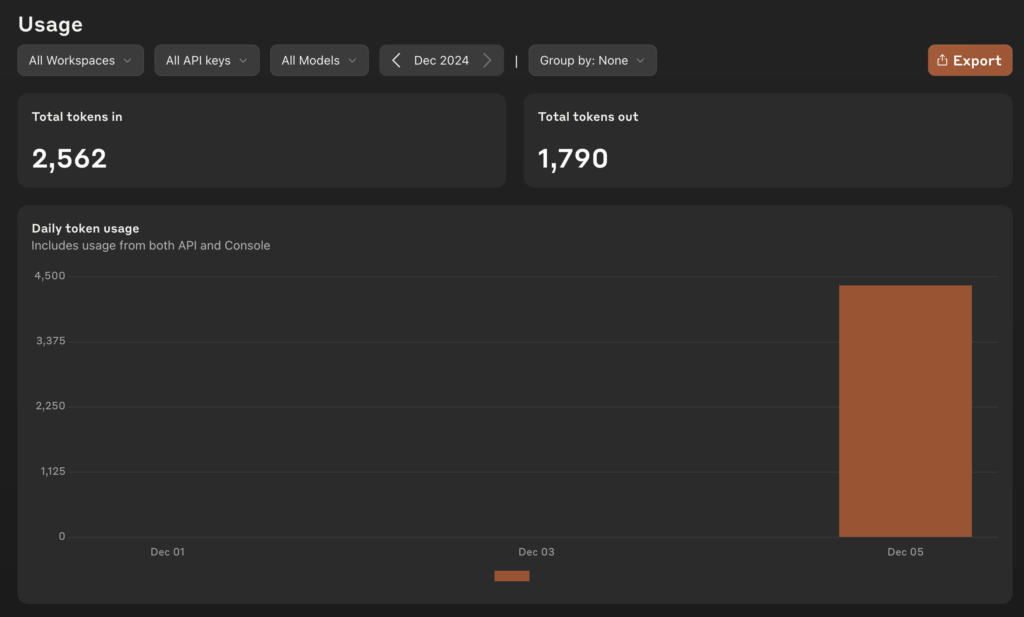
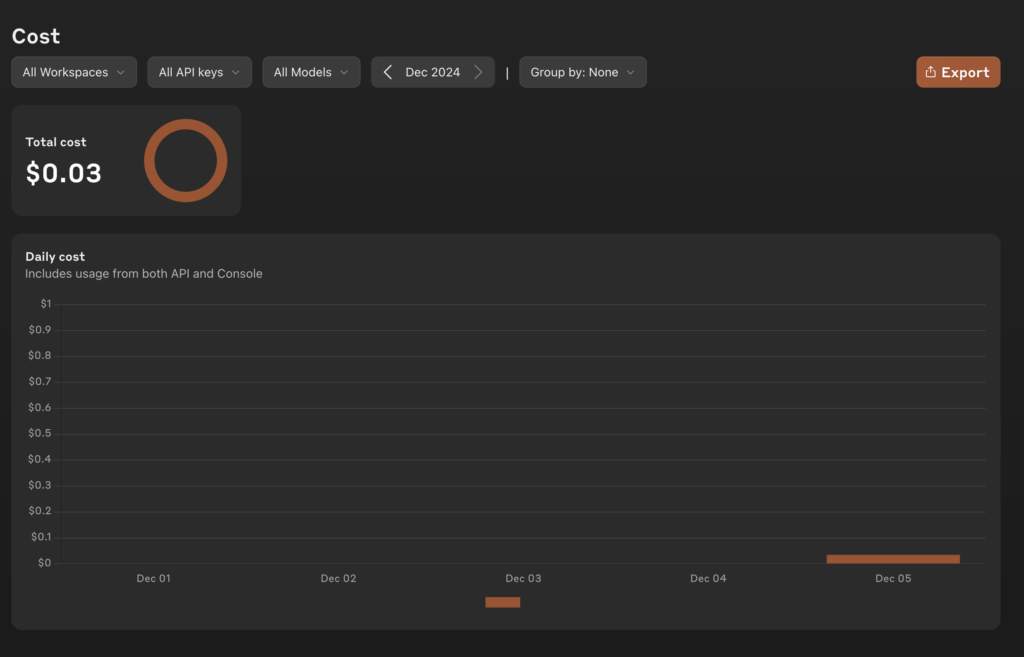
Kết quả:
(venv) (base) taipm@Phans-MacBook-Pro autogen_chat_conversation % python app1.py
flaml.automl is not available. Please install flaml[automl] to enable AutoML functionalities.
Student_Agent (to Teacher_Agent):
Số phức là gì?
--------------------------------------------------------------------------------
>>>>>>>> USING AUTO REPLY...
/Users/taipm/GitHub/autogen_chat_conversation/venv/lib/python3.12/site-packages/autogen/oai/anthropic.py:420: UserWarning: Cost calculation not available for model claude-3-5-sonnet-20241022
warnings.warn(f"Cost calculation not available for model {model}", UserWarning)
Teacher_Agent (to Student_Agent):
Tôi sẽ giải thích về số phức một cách đơn giản:
Số phức là một dạng số mở rộng từ số thực, được tạo thành từ hai phần:
1. Phần thực (a)
2. Phần ảo (bi), trong đó i là đơn vị ảo và i² = -1
Dạng tổng quát của số phức là: z = a + bi
Ví dụ:
- 3 + 2i là một số phức
- 4 - 5i là một số phức
- 2 + 0i = 2 (số thực thuần túy)
- 0 + 3i = 3i (số thuần ảo)
Số phức được tạo ra để giải quyết các bài toán không thể giải được trong tập số thực, như:
- Phương trình x² + 1 = 0
- Căn bậc hai của số âm
Một số phức có thể được biểu diễn:
1. Dạng đại số: z = a + bi
2. Dạng lượng giác: z = r(cosφ + isinφ)
3. Trên mặt phẳng phức (còn gọi là mặt phẳng Gauss)
Số phức có nhiều ứng dụng trong:
- Điện học
- Cơ học lượng tử
- Xử lý tín hiệu
- Và nhiều lĩnh vực khoa học kỹ thuật khác
--------------------------------------------------------------------------------
>>>>>>>> USING AUTO REPLY...
Student_Agent (to Teacher_Agent):
Cảm ơn bạn đã giải thích rõ ràng về số phức. Tôi có một số câu hỏi:
1. Làm thế nào để thực hiện các phép tính cơ bản với số phức (cộng, trừ, nhân, chia)?
2. Thế nào là số phức liên hợp và nó có ý nghĩa gì?
3. Làm sao để tính môđun (độ lớn) của một số phức?
4. Trong mặt phẳng Gauss, trục hoành và trục tung biểu diễn những gì?
Bạn có thể giải thích giúp tôi những điều này không?
--------------------------------------------------------------------------------
>>>>>>>> USING AUTO REPLY...
Teacher_Agent (to Student_Agent):
Tôi sẽ giải thích từng câu hỏi:
1. Các phép tính với số phức:
- Cộng/Trừ: Cộng/trừ riêng phần thực và phần ảo
(a + bi) ± (c + di) = (a ± c) + (b ± d)i
Ví dụ: (3 + 2i) + (1 - 4i) = 4 - 2i
- Nhân: Áp dụng phép nhân đa thức và nhớ i² = -1
(a + bi)(c + di) = (ac - bd) + (ad + bc)i
Ví dụ: (2 + 3i)(1 + i) = 2 + 2i + 3i + 3i² = 2 + 5i - 3 = -1 + 5i
- Chia: Nhân cả tử và mẫu với số phức liên hợp của mẫu
(a + bi)/(c + di) = [(a + bi)(c - di)]/[(c + di)(c - di)]
Ví dụ: (4 + 2i)/(2 + i) = (4 + 2i)(2 - i)/(2² + 1²) = (8 + 4i - 2i - i²)/5 = (8 + 2i + 1)/5 = (9 + 2i)/5
2. Số phức liên hợp:
- Của số phức z = a + bi là z̄ = a - bi
- Ý nghĩa:
+ Tích của số phức và liên hợp của nó là một số thực
+ Dùng trong phép chia số phức
+ z × z̄ = a² + b²
3. Môđun của số phức:
- Môđun của z = a + bi là |z| = √(a² + b²)
- Đây chính là khoảng cách từ điểm biểu diễn số phức đến gốc tọa độ trong mặt phẳng Gauss
- Ví dụ: |3 + 4i| = √(3² + 4²) = √25 = 5
4. Mặt phẳng Gauss:
- Trục hoành (trục x): biểu diễn phần thực
- Trục tung (trục y): biểu diễn phần ảo
- Mỗi điểm (a,b) biểu diễn số phức z = a + bi
- Điểm có tọa độ (a,b) cách gốc tọa độ một khoảng bằng môđun của số phức
--------------------------------------------------------------------------------
ChatResult(chat_id=None, chat_history=[{'content': 'Số phức là gì?', 'role': 'assistant'}, {'content': 'Tôi sẽ giải thích về số phức một cách đơn giản:\n\nSố phức là một dạng số mở rộng từ số thực, được tạo thành từ hai phần:\n1. Phần thực (a)\n2. Phần ảo (bi), trong đó i là đơn vị ảo và i² = -1\n\nDạng tổng quát của số phức là: z = a + bi\n\nVí dụ:\n- 3 + 2i là một số phức\n- 4 - 5i là một số phức\n- 2 + 0i = 2 (số thực thuần túy)\n- 0 + 3i = 3i (số thuần ảo)\n\nSố phức được tạo ra để giải quyết các bài toán không thể giải được trong tập số thực, như:\n- Phương trình x² + 1 = 0\n- Căn bậc hai của số âm\n\nMột số phức có thể được biểu diễn:\n1. Dạng đại số: z = a + bi\n2. Dạng lượng giác: z = r(cosφ + isinφ)\n3. Trên mặt phẳng phức (còn gọi là mặt phẳng Gauss)\n\nSố phức có nhiều ứng dụng trong:\n- Điện học\n- Cơ học lượng tử\n- Xử lý tín hiệu\n- Và nhiều lĩnh vực khoa học kỹ thuật khác', 'role': 'user'}, {'content': 'Cảm ơn bạn đã giải thích rõ ràng về số phức. Tôi có một số câu hỏi:\n\n1. Làm thế nào để thực hiện các phép tính cơ bản với số phức (cộng, trừ, nhân, chia)?\n\n2. Thế nào là số phức liên hợp và nó có ý nghĩa gì?\n\n3. Làm sao để tính môđun (độ lớn) của một số phức?\n\n4. Trong mặt phẳng Gauss, trục hoành và trục tung biểu diễn những gì?\n\nBạn có thể giải thích giúp tôi những điều này không?', 'role': 'assistant', 'name': 'Student_Agent'}, {'content': 'Tôi sẽ giải thích từng câu hỏi:\n\n1. Các phép tính với số phức:\n- Cộng/Trừ: Cộng/trừ riêng phần thực và phần ảo\n (a + bi) ± (c + di) = (a ± c) + (b ± d)i\n Ví dụ: (3 + 2i) + (1 - 4i) = 4 - 2i\n\n- Nhân: Áp dụng phép nhân đa thức và nhớ i² = -1\n (a + bi)(c + di) = (ac - bd) + (ad + bc)i\n Ví dụ: (2 + 3i)(1 + i) = 2 + 2i + 3i + 3i² = 2 + 5i - 3 = -1 + 5i\n\n- Chia: Nhân cả tử và mẫu với số phức liên hợp của mẫu\n (a + bi)/(c + di) = [(a + bi)(c - di)]/[(c + di)(c - di)]\n Ví dụ: (4 + 2i)/(2 + i) = (4 + 2i)(2 - i)/(2² + 1²) = (8 + 4i - 2i - i²)/5 = (8 + 2i + 1)/5 = (9 + 2i)/5\n\n2. Số phức liên hợp:\n- Của số phức z = a + bi là z̄ = a - bi\n- Ý nghĩa: \n + Tích của số phức và liên hợp của nó là một số thực\n + Dùng trong phép chia số phức\n + z × z̄ = a² + b²\n\n3. Môđun của số phức:\n- Môđun của z = a + bi là |z| = √(a² + b²)\n- Đây chính là khoảng cách từ điểm biểu diễn số phức đến gốc tọa độ trong mặt phẳng Gauss\n- Ví dụ: |3 + 4i| = √(3² + 4²) = √25 = 5\n\n4. Mặt phẳng Gauss:\n- Trục hoành (trục x): biểu diễn phần thực\n- Trục tung (trục y): biểu diễn phần ảo\n- Mỗi điểm (a,b) biểu diễn số phức z = a + bi\n- Điểm có tọa độ (a,b) cách gốc tọa độ một khoảng bằng môđun của số phức', 'role': 'user', 'name': 'Teacher_Agent'}], summary={'content': '5. Một số tính chất quan trọng của số phức:\n\n- Môđun của tích bằng tích của các môđun: |z₁ × z₂| = |z₁| × |z₂|\n\n- Môđun của thương bằng thương của các môđun: |z₁/z₂| = |z₁|/|z₂|\n\n- Bất đẳng thức tam giác: |z₁ + z₂| ≤ |z₁| + |z₂|\n\n6. Dạng lượng giác của số phức:\n- z = r(cosφ + isinφ), trong đó:\n + r là môđun của số phức\n + φ là argument (góc với trục thực)\n- r = √(a² + b²)\n- φ = arctan(b/a) (cần xét dấu để xác định góc đúng)\n\n7. Công thức Euler:\n- e^(iφ) = cosφ + isinφ\n- Số phức có thể viết dưới dạng: z = re^(iφ)\n\n8. Các nghiệm của phương trình z^n = 1:\n- Có n nghiệm phân bố đều trên đường tròn đơn vị\n- Được gọi là nghiệm căn đơn vị thứ n\n\nNhững kiến thức này rất quan trọng trong nhiều ứng dụng thực tế của số phức.', 'refusal': None, 'role': 'assistant', 'audio': None, 'function_call': None, 'tool_calls': None}, cost={'usage_including_cached_inference': {'total_cost': 0.0, 'claude-3-5-sonnet-20241022': {'cost': 0.0, 'prompt_tokens': 2562, 'completion_tokens': 1790, 'total_tokens': 4352}}, 'usage_excluding_cached_inference': {'total_cost': 0.0, 'claude-3-5-sonnet-20241022': {'cost': 0.0, 'prompt_tokens': 2562, 'completion_tokens': 1790, 'total_tokens': 4352}}}, human_input=[])